What Is the Most Important Mathematical Equation?
- Olivia Crew
- Oct 26, 2022
- 5 min read
Math is a long, tedious, steady effort with occasional breakthroughs; it's more like a marathon than a sprint. We occasionally experience those coveted "Eureka" moments, those little strings of letters and numbers that fundamentally alter the course of research. Here are a few well-known equations, ranging from classical Greek math to contemporary physics.

Pythagoras’s theorem (530 BC)
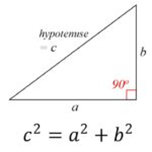
One of the fundamental principles of geometry is that the square of the hypotenuse, or side opposite the right angle, in a right triangle, equals the sum of the squares of the other two sides. Although there is some indication that Babylonian mathematicians were aware of the formula, the idea is typically credited to the Greek mathematician Pythagoras. It's also conceivable that he was the first to demonstrate a theorem that many others were aware of.
The number of proofs for the theorem may be the highest of any mathematical theorem. They are quite varied. Some go back thousands of years and include both algebraic and geometric proofs.
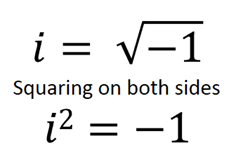
Gerolamo Cardano, an Italian mathematician, is credited with creating complex numbers as the first one, at the time labelling them "fictitious." However, Leonhard Euler, one of the most significant mathematicians and scientists in human history, is credited with developing the concept of I in mathematics as the fictitious number representing the square root of -1.
Complex numbers are essentially imaginary numbers that are incredibly helpful for many computations while not existing. They have practical applications in many disciplines, including physics, chemistry, biology, economics, electrical engineering, and statistics. They are composed of numbers with a real portion (the numbers we are all familiar with) and an imaginary part (the I depicted above).
The logarithms

In essence, logarithms are the exponentiation function in reverse. You require a base (a), a number (N), and a logarithm (x) of N in base a, where N is equal to a to the power of x. Although logarithms appear to be just another way to express the same thing, they have a wide range of useful applications in fields including psychology, economics, and the measurement of several physical phenomena (such as pH or earthquake magnitude).
In a publication with the appropriately named Mirifici Logarithm rum Canon is Description (Description of the Wonderful Rule of Logarithms), John Napier officially introduced logarithms in 1614. The natural logarithm, or e, is a particular type of logarithm with transcendence and irrationality properties. Its value is around 2.71828182845. Although that's a story for another day, e itself has a fascinating history and a staggering amount of uses.
Calculus
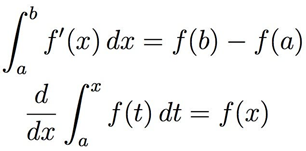
Calculus has had a greater mathematical effect than most other areas. Calculus, which was created in the 17th century by Gottfried Wilhelm Leibniz and Isaac Newton, is extensively utilized in science, engineering, and economics. Dealing with tiny quantities, especially infinitely small ones, is the main emphasis of calculus. Even though they are theoretically indefinitely tiny, they can be considered real numbers in calculus.
Integration, as seen above, may be visualized as measuring the area under a curve described by a function.
The Law of Gravity

Newton is also "responsible" for the law of gravity, one of the most well-known and magnificent equations in the entire world.
In essence, the law explains how any two bodies with masses m1 and m2 are drawn to one another. The fair distance between them determines the force (F1, F2) in an inverse proportion (r). A gravitational constant, G, is the lone component still present. It's still unclear what this constant is.
General Relativity
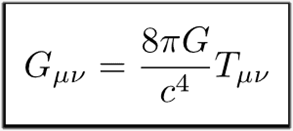
Newton's law established our level of mechanical understanding for about 200 years. These two accomplishments stand on the greatest pedestals in the field of physics, and Einstein's work in the 20th century advanced things much further.
General relativity, which generalizes Newton's theory and offers a coherent account of gravity as a geometric attribute of space and time, or spacetime, is a geometric theory of gravitation. In particular, Einstein demonstrated a concept known as "spacetime" that unites the three spatial dimensions with the temporal dimension and that this spacetime can be bent by gravity, with the curvature being inversely proportional to the energy and momentum of any present matter and radiation.
Second law of thermodynamics
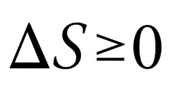
We cannot have pleasant things in the universe due to the Second Law of Thermodynamics. Putting jokes aside, the temperature, energy, and entropy that describe thermodynamic systems are defined by the four laws of thermodynamics. Here, the second one, in particular, shines out because of its clarity and enormous consequences.
In essence, the rule implies that the total entropies of all thermodynamic systems that interact must continually rise or, at best, remain constant. A closed system's entropy (or disorder) grows as energy transforms into another form or when matter moves. All temperature, pressure, and density variances eventually flatten out.
Maxwell’s Equations
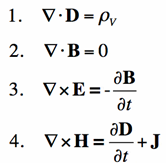
Expressed, Newton's law is to mechanics what Maxwell's equations are to electromagnetic. They provide classical electromagnetism, classical optics, and electric circuits with a mathematical foundation. They are essentially present in every electronic gadget, even the one you are reading this on.
According to Maxwell's laws, charges, currents, and changes in the fields produce electric and magnetic fields. The proof that magnetic and electric fields spread at the speed of light greatly advanced.
Euler’s Identity
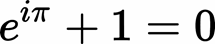
Last but not least, this is conceivably the most beautiful equation because it uses all the "basic" numbers:
0, which is neutral for addition and subtraction;
1, which is neutral for multiplication and division;
e, which is Euler's number (see above),
the foundation of natural logarithms;
I which is the imaginary unit (see above);
Which is pi, the reciprocal of the ratio of a circle's circumference to its diameter
Why should you pick our academic writers for Online Assignment Help Service in UK?
There are many assignment writers in UK, but not all offer the same outstanding online assignment help service in UK that our team of qualified academic writers does. If so, you should contact LiveWebTutors and decide whether to employ an assignment helper for the following reasons.
UK writers who are natives
Only local authors, in our opinion, will be able to produce error-free, premium-quality work. Therefore, LiveWebTutors has a specialized staff of UK native assignment assistants to help you. Additionally, most of our team's assignment writers are graduates of prestigious UK colleges.
Outstanding custom writing
We strive to please our consumers to gain their confidence. Therefore, the assignment writing specialists on our team will create a great customized assignment paper following the agreed-upon requirements to delight our consumers. Most significantly, our professionals will use references from trusted sources while composing projects.
Online assignment help that is affordable
Generally, it is hard to obtain high-caliber work from academic writers with a Ph.D. for a reasonable price. But with LiveWebTutors, you may get the greatest assignment help online at a reasonable price for nearly all topic assignments.
Excellent writing that's free of plagiarism




Comments